Model complexity as a function of sample size

Andrew Gelman’s blog post gives me ideas. http://andrewgelman.com/2012/10/model-complexity-as-a-function-of-sample-size/#comment-105823 

I’m just going to reproduce the whole thing below.

So what’s my idea?

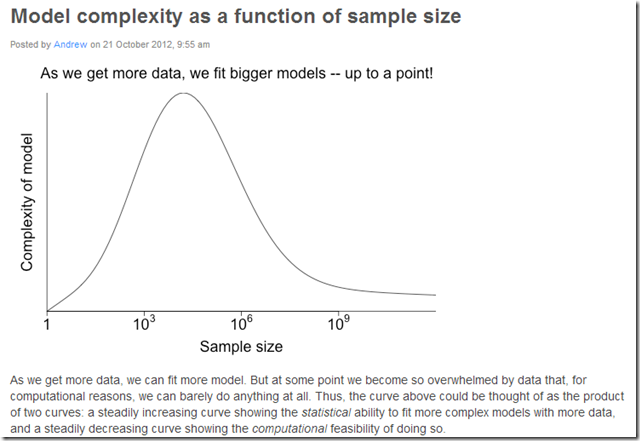
I’m assuming this is a conceptual graph and there’s no existing evidence for the precise shape of the curve or the approximate optimal point, but I’d be happy to be corrected on this.

This also gives me an idea. I’ve been distributing a data set to marketing and economics academics that’s large (about 70 gig), but I notice that the papers (several dozen so far) only seem to use tiny pieces of it, although the models they use are often complex. This would potentially provide a way to look at a related curve — the size of the data used on the x axis, and the complexity of the model on the y axis. (The size of the potential usable data is fixed.)

The size of the data used would be relatively easy to measure.

The complexity of the model is a harder concept, especially since the models are looking at a variety of different phenomena using a variety of different approaches and published in a variety of venues.

Can someone point me to some way to measure model complexity? Say, if you took a random set of papers from a journal on different topics and wanted to do this? That’s an analogous task because the issues addressed by those using this data range rather broadly. My first thought would be to use some set of low-level experts (Mechanical Turk?) to evaluate the papers in a pairwise fashion, and then generate something like an ELO score in chess (the most complex model “winning”). That’s not fully satisfactory because bad writers will seem more complex, good writers will seem more simple, I would guess.

If anyone is interested in discussing this, contact me.